How To Calculate The Hypotenuse Of A Right Triangle: A Simple Guide

Calculating the hypotenuse of a right triangle might sound like a math challenge, but it’s simpler than you think. Whether you’re brushing up on your geometry skills or solving real-life problems, understanding this concept can come in handy. The hypotenuse is the longest side of a right triangle, and it plays a crucial role in various fields, from construction to physics. So, buckle up, because we’re diving deep into the world of triangles!

Now, imagine this: you’re building a ramp, designing a roof, or just trying to ace your math test. Knowing how to calculate the hypotenuse can make all the difference. This guide will break it down step by step, making it easy for anyone to grasp. No need to panic if math isn’t your strongest suit—we’ve got you covered.

So, why is the hypotenuse so important? Well, it’s not just about triangles. It’s about understanding relationships between numbers, shapes, and the world around us. Let’s explore how this simple concept can unlock complex solutions. Ready to dive in? Let’s go!

Understanding the Basics of Right Triangles

Before we jump into calculating the hypotenuse, let’s get familiar with the basics. A right triangle is a triangle that has one angle measuring exactly 90 degrees. This special angle is what makes it unique. The sides of a right triangle have specific names: the two shorter sides are called the legs, and the longest side is the hypotenuse.

What Makes a Triangle "Right"?

A triangle is considered "right" when it contains one 90-degree angle. This angle is often marked with a small square in diagrams to make it stand out. The other two angles in a right triangle must add up to 90 degrees, ensuring the total sum of all angles equals 180 degrees.

Key Features of a Right Triangle

• One 90-degree angle
• Two shorter sides (legs)
• One longest side (hypotenuse)

These features are essential to understanding how the hypotenuse works. The hypotenuse is always opposite the right angle, making it the longest side in the triangle.

Why the Hypotenuse Matters

The hypotenuse isn’t just a fancy math term; it’s a critical component in many real-world applications. From construction to navigation, the hypotenuse helps us solve problems involving distances and angles.

Applications of the Hypotenuse

Here are a few examples where calculating the hypotenuse comes in handy:

• Construction: Builders use the hypotenuse to ensure structures are stable and aligned.
• Navigation: Pilots and sailors calculate distances using the hypotenuse in triangular paths.
• Physics: Scientists use the hypotenuse to analyze motion and forces in right triangles.

Understanding the hypotenuse opens doors to solving practical problems in everyday life. It’s not just about math—it’s about applying math to the world around us.

Introducing the Pythagorean Theorem

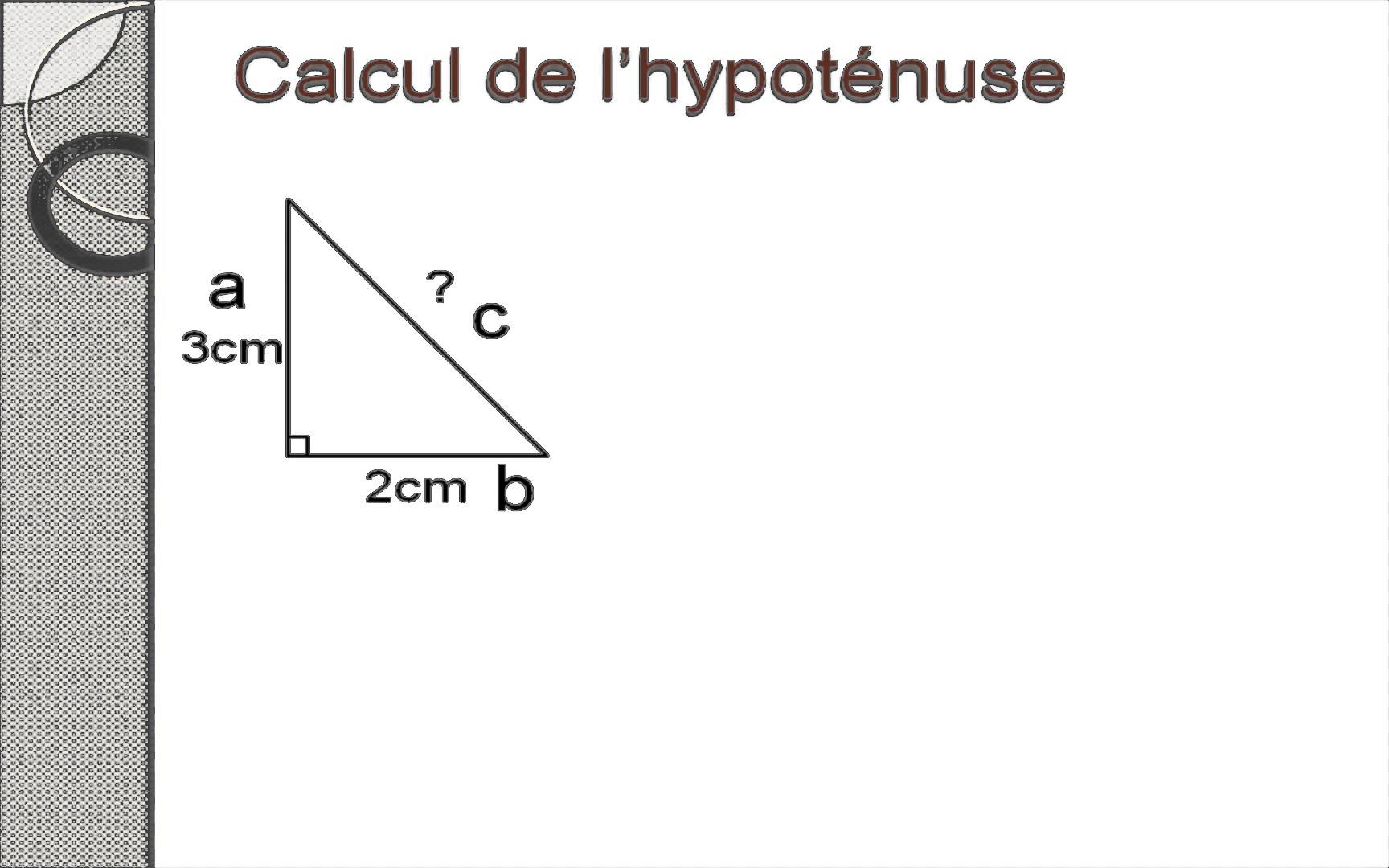
The Pythagorean Theorem is the backbone of calculating the hypotenuse. This ancient mathematical principle states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In equation form, it looks like this:

c² = a² + b²

Where:

• c is the hypotenuse
• a and b are the two legs of the triangle

This theorem is the key to unlocking the mystery of the hypotenuse. Let’s break it down further.

Breaking Down the Pythagorean Theorem

Here’s how the theorem works:

1. Square the lengths of the two legs (a² and b²).
2. Add the squared values together.
3. Take the square root of the result to find the hypotenuse (c).

It’s as simple as that! This formula has been used for thousands of years and remains one of the most powerful tools in geometry.

Step-by-Step Guide to Calculating the Hypotenuse

Now that you know the theory, let’s put it into practice. Follow these steps to calculate the hypotenuse of any right triangle:

Step 1: Identify the Legs

First, determine the lengths of the two legs of the triangle. These are the two shorter sides that form the right angle. Let’s call them a and b.

Step 2: Square the Legs

Next, square the lengths of the legs. Multiply each leg by itself to get a² and b².

Step 3: Add the Squares

Add the squared values together to get the sum. This sum represents the square of the hypotenuse.

Step 4: Find the Square Root

Finally, take the square root of the sum to find the length of the hypotenuse. This is your answer!

Let’s look at an example:

• Leg a = 3
• Leg b = 4

Square the legs:

• a² = 3 × 3 = 9
• b² = 4 × 4 = 16

Add the squares:

• 9 + 16 = 25

Take the square root:

• c = √25 = 5

So, the hypotenuse is 5 units long!

Common Mistakes to Avoid

Even with a simple formula like the Pythagorean Theorem, mistakes can happen. Here are a few common pitfalls to watch out for:

• Forgetting to square the legs: Make sure you multiply each leg by itself before adding them together.
• Adding the legs instead of squaring them: Always square the legs first!
• Skipping the square root: Don’t forget to take the square root of the sum to find the hypotenuse.

Double-check your calculations to ensure accuracy. Practice makes perfect!

Advanced Techniques for Complex Triangles

What if you’re dealing with a more complex triangle? Don’t worry—there are advanced techniques to help you out. For example, if you know one leg and the hypotenuse, you can rearrange the Pythagorean Theorem to solve for the missing leg:

a² = c² - b²

Or, if you know the angles, you can use trigonometric functions like sine, cosine, or tangent to find the hypotenuse. These methods are especially useful in fields like engineering and architecture.

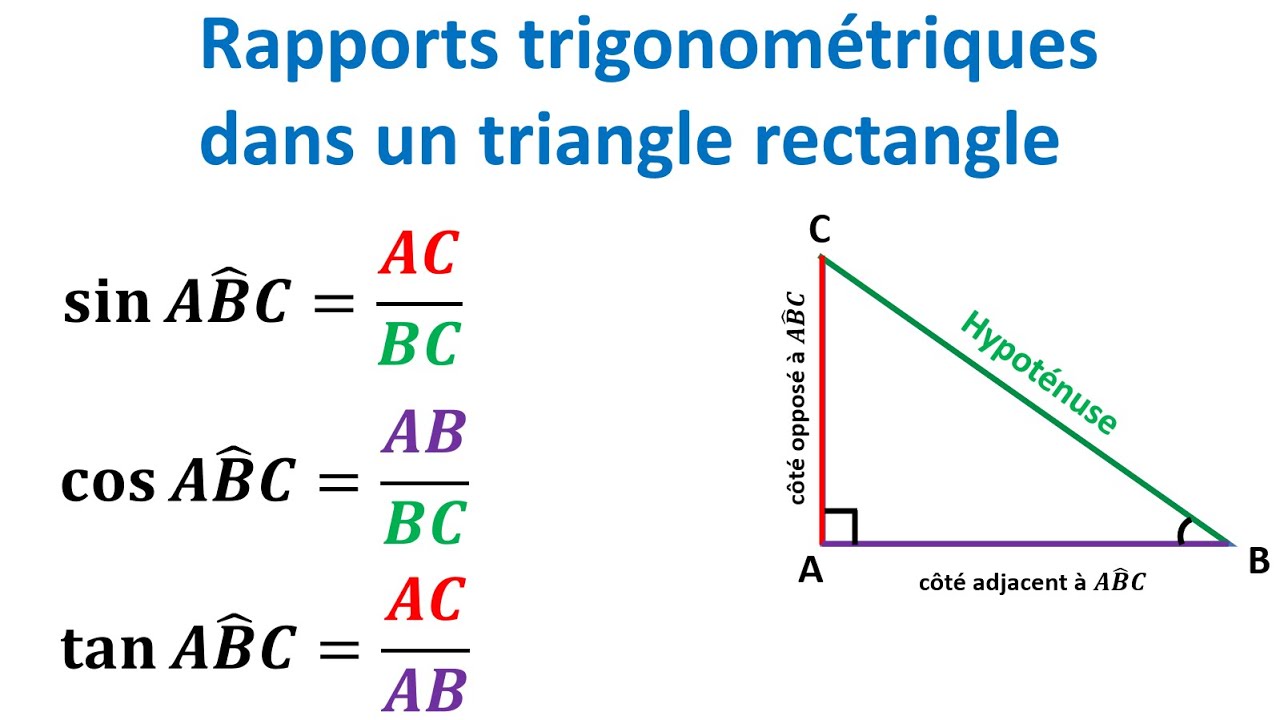
Using Trigonometry

Trigonometry offers another way to calculate the hypotenuse. If you know one angle (other than the right angle) and the length of one side, you can use sine, cosine, or tangent to find the hypotenuse. For example:

• sin(θ) = opposite/hypotenuse
• cos(θ) = adjacent/hypotenuse
• tan(θ) = opposite/adjacent

By rearranging these formulas, you can solve for the hypotenuse. Trigonometry adds another layer of versatility to your math toolkit.

Real-Life Examples of Hypotenuse Calculations

Let’s explore some real-world scenarios where calculating the hypotenuse is essential:

Example 1: Building a Ramp

Imagine you’re designing a ramp for a wheelchair. The ramp needs to rise 3 feet and extend 4 feet horizontally. To ensure safety, you need to calculate the length of the ramp (the hypotenuse). Using the Pythagorean Theorem:

• c² = 3² + 4²
• c² = 9 + 16
• c² = 25
• c = √25 = 5

The ramp needs to be 5 feet long.

Example 2: Navigating a Boat

A sailor needs to calculate the distance between two points on a triangular path. If the two legs of the triangle are 6 miles and 8 miles, the hypotenuse represents the direct distance:

• c² = 6² + 8²
• c² = 36 + 64
• c² = 100
• c = √100 = 10

The sailor’s direct distance is 10 miles.

Tips for Mastering Hypotenuse Calculations

Here are some tips to help you master calculating the hypotenuse:

• Practice regularly: The more you practice, the more comfortable you’ll become with the Pythagorean Theorem.
• Use tools: Calculators and math apps can help you verify your answers quickly.
• Visualize the triangle: Drawing a diagram can make it easier to understand the relationships between the sides.
• Break down complex problems: If the problem seems overwhelming, break it into smaller steps.

With these tips, you’ll be calculating hypotenuses like a pro in no time!

Conclusion

Calculating the hypotenuse of a right triangle is a valuable skill that extends beyond the classroom. From construction to navigation, this concept plays a crucial role in solving real-world problems. By mastering the Pythagorean Theorem and practicing regularly, you can unlock the power of geometry.

So, what are you waiting for? Start practicing today and see how far you can go. Leave a comment below with your own examples or questions, and don’t forget to share this guide with your friends. Together, we can make math fun and accessible for everyone!

Table of Contents

• Understanding the Basics of Right Triangles
• Why the Hypotenuse Matters
• Introducing the Pythagorean Theorem
• Step-by-Step Guide to Calculating the Hypotenuse
• Common Mistakes to Avoid
• Advanced Techniques for Complex Triangles
• Real-Life Examples of Hypotenuse Calculations
• Tips for Mastering Hypotenuse Calculations
• Conclusion

Details

Comment Calculer Un Triangle Rectangle Image to u

Details

Comment calculer l'hypoténuse d'un triangle rectangle

Details

Comment calculer les angles d'un triangle rectangle